Spatial vectors

In RobCoGen, 6D coordinate vectors representing spatial-vectors (twists and wrenches) always follow this convention:

• the first three coordinates represent the angular part of the quantity (either angular velocity or torque)
• the last three coordinates represent the linear part (linear velocity or force)

As far as C++ is concerned, the iit::rbd namespace has some elements to abstract the underlying convention, like a 6-value enum to index symbolically the vectors. Whenever possible, user code should use these tools rather than relying on the convention.

Reference frames

The coordinate frames of links and joints are not mentioned explicitly in model files (see the example above). In RobCoGen, the identifier of a reference frame (i.e. its name) defaults to the name of the link or the joint it refers to, with the prefix fr_.

For example, if a link of the robot is called lowerLeg in the model, the name of the default reference frame for that link would be fr_lowerLeg. Names in this form appear in the generated code in the identifiers of coordinate transforms.

Coordinate transformation matrices

Coordinate transforms, in the generated code but also in documentation, follow a naming convention in the form:

A_X_B

where A and B represent two arbitrary reference frames. With this notation it is immediate to understand the effect of the transform: when right-multiplied by a column vector of coordinates in frame B it gives the coordinates in frame A, as in v_A = A_X_B * v_B

For example, the transform that maps coordinates in the frame of a link called wrist to coordinates of link trunk, will typically appear in the source code with the identifier fr_trunk_X_fr_wrist.

In the notation A_X_B, the frames A and B are sometimes referred to as the left and right frame, respectively, because of their relative position with respect to X. The figure below illustrates the notation.

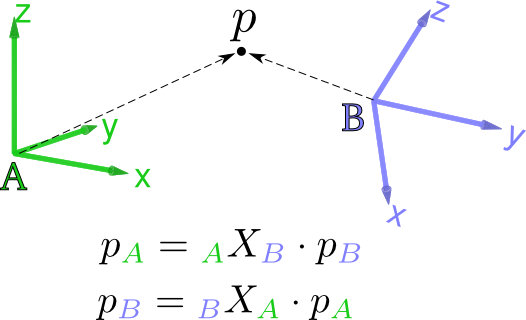
In the figure, in the first equation A is the left frame while B is the right frame. In the second equation it is the other way round.

Given a certain context, a pair right/left frame uniquely identifies the semantics of a coordinate transform.

Jacobians

The convention of linear/angular coordinates of spatial vectors is reflected also in the geometric Jacobians generated by RobCoGen. Jacobians have 6 rows, the top three correspond to the angular velocity, while the bottom three correspond to the linear velocity.

Note, however, that Jacobians in RobCoGen are not spatial. They do not map to spatial velocities, but to 6D vectors that are simply the composition of two 3D Euclidean vectors, stacked together. These two vectors are the angular and linear velocity of a certain point on a body, expressed in a reference frame. This definition is the most common in classical robotics (cfr. for example Siciliano et al., "Robotics", Springer 2009).

For example, a Jacobian called B_J_P gives the velocity of the origin of frame P expressed with coordinates of frame B, in the Euclidean sense (that is, the actual linear velocity of P is only rotated to be expressed with coordinates in B, regardless of the relative position of the two origins).