Overview

The kinematics/dynamics model of an articulated robot is the primary input of RobCoGen. The format of robot models is text with a simple syntax tailored for the domain. The language is called Kinematics-DSL (DSL stands for Domain Specific Language), and it is documented in this page.

The logical structure of a file ("document", or "model") is the following:

Robot <name>

  <link 0 spec> // the robot base
  <link 1 spec>
  //...
  <link n spec>

  <joint 1 spec>
  //...
  <joint n spec>

Any link block contains an id, the inertia properties, and a possibly empty list of children links. The geometrical constants of the robot are encoded in the joint parameters, which are extensively explained below.

The format allows to model any kinematic tree, that is a mechanism where each rigid body has one and only one parent (except the base), but can have multiple children.

Example

Here is the sample robot model file included in the distribution of RobCoGen:

Robot Fancy
{
/*
 * A fictitious kinematic chain, without branches.
 * All the links are hollow cylinders infinitely thin (internal and
 * external radii are the same) with radius equal to 0.05 meters,
 * unit length, unit mass.
 * They are connected by five joints: revolute, prismatic, revolute,
 * prismatic, revolute.
*/

RobotBase base0 {
    inertia_properties {
        mass = 1.0
        CoM = (0.0, 0.0, 0.0)
        Iy=0.0  Ix=0.0  Ixy=0.0 Iz=0.0  Ixz=0.0 Iyz=0.0
    }
    children {
        link1 via jA
    }
}

link link1 {
    id = 1
    inertia_properties {
        mass = 1.0
        CoM = (0.5, .0, .0)
        Ix=0.0025  Iy=0.33458  Iz=0.33458  Ixy=0.0  Ixz=0.0  Iyz=0.0
    }
    children {
        link2 via jB
    }
}

link link2 {
    id = 2
    inertia_properties {
        mass = 1.0
        CoM = (0.0, 0.0, 0.5)
        Ix=0.33458  Iy=0.33458  Iz=0.0025  Ixy=0.0  Ixz=0.0  Iyz=0.0
    }
    children {
        link3 via jC
    }
}

link link3 {
    id = 3
    inertia_properties {
        mass = 1.0
        CoM = (0.5, .0, .0)
        Ix=0.0025  Iy=0.33458  Iz=0.33458  Ixy=0.0  Ixz=0.0  Iyz=0.0
    }
    children {
        link4 via jD
    }
}

link link4 {
    id = 4
    inertia_properties {
        mass = 1.0
        CoM = (0.0, 0.0, 0.5)
        Ix=0.33458  Iy=0.33458  Iz=0.0025  Ixy=0.0  Ixz=0.0  Iyz=0.0
    }
    children {
        link5 via jE
    }
}

link link5 {
    id = 5
    inertia_properties {
        mass = 1.0
        CoM = (0.5, .0, .0)
        Ix=0.0025  Iy=0.33458  Iz=0.33458  Ixy=0.0  Ixz=0.0  Iyz=0.0
    }
    children {}
    frames {
       ee {
           translation = (1.0, 0.0, 0.0)
           rotation    = (0.0, 0.0, 0.0)
       }
    }
}


r_joint jA {
    ref_frame {
        translation = (0.0, 0.0, 0.0)
        rotation = (0.0, 0.0, 0.0)
    }
}

p_joint jB {
    ref_frame {
        translation = (1.0, 0.0, 0.0)
        rotation = (-PI/2.0, 0.0, 0.0)
    }
}

r_joint jC {
    ref_frame {
        translation = (0.0, 0.0, 1.0)
        rotation = (0.0, 0.0, 0.0)
    }
}

p_joint jD {
    ref_frame {
        translation = (1.0, 0.0, 0.0)
        rotation = (PI/2.0, 0.0, 0.0)
    }
}

r_joint jE {
    ref_frame {
        translation = (0.0, 0.0, 1.0)
        rotation = (0.0, 0.0, 0.0)
    }
}


}

Here is an illustration of the same robot, Fancy, taken from a simulation using RobCoGen-generated code. Spheres represent revolute joints, cubes prismatic ones.

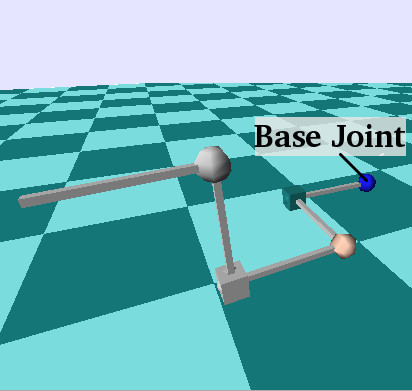
Geometry

This section walks you through the procedure required to model an articulated mechanism with the Kinematics-DSL. It explains how to place the coordinate frames and how to measure lengths and angles. The convention about the placement of reference frames (or "coordinate frames") is definitely the aspect that can be most confusing, and that is typically not documented enough. I tried to avoid such a mistake.

First, the definition of some of the terms use in the text:

• A kinematic-pair is a pair of links connected by a joint

• The links of a pair, in relation with the joint, are called predecessor and successor.

• The links of a pair, in relation with each other, are called parent and child.

• We say that a parent/predecessor/joint supports the child/joint/successor; the opposite relation is supported by.

Basic modeling

The following applies to kinematic trees (no loops), with one-dof joints only.

1. Ordering. Set the topological ordering for the kinematic tree of your robot: which link is the base, which are the parents/children, etc. This choice induces a total ordering with respect to the relation supports/supported by.

2. Zero configuration. Choose the configuration of the robot you wish to identify with the zero joint-status vector; consider the robot assembled, but neglect joint limits. That is, the zero configuration must comply with the holonomic constraints of the real joints, but it need not respect the range of motion; it might very well be unreachable by the actual robot.¹ (Note that no reference frame was mentioned yet.)

3. Link-frames. Consider each individual link (in isolation), and attach a Cartesian frame to it. The Z axis must lie along the axis of the supporting joint (e.g. the Z axis of a forearm is the elbow axis), but you are otherwise free to choose the pose.² The link-frame of the base link of the robot can be placed anywhere.

4. Joint-frames. Consider the robot assembled, freezed in the zero configuration. For each joint of the robot, attach a new frame onto its predecessor, in the same pose of the frame of its successor (i.e. the two frames coincide). This is the joint-frame.

5. Geometrical properties. The pose of any joint-frame relative to the predecessor-frame is a geometrical constant of the robot. This pose is represented in the joint sections of a Kinematics-DSL model.

Example

Let's consider a simple kinematic pair, as the extension to a general tree would simply require to reiterate the same steps. These screenshots show the links and the ideal joint axes (in red):

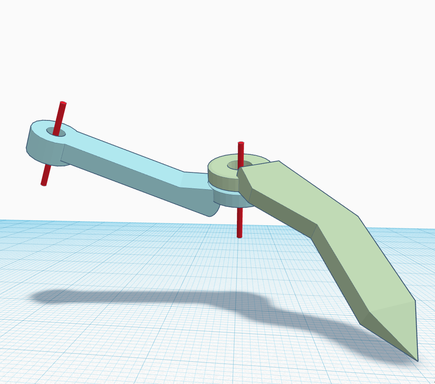
The corresponding section of a model would look like this:

// ...

link Blue {
    id = <i>
    inertia_properties {
        // ...
    }
    children {
        Green via TheJoint
    }
}

link Green {
    id = <i+1>
    inertia_properties {
        // ...
    }
    children { }
}

r_joint TheJoint { // 'r_' stands for revolute
    ref_frame {
        // ...
    }
}

1. Ordering. We choose the blue link to be the parent (and therefore the predecessor of the joint).

2. Zero configuration. Here are some possibilities:

The choice of the zero configuration is entirely arbitrary, pick an intuitive one in the context of your application.

3. Link-frames. In the examples below, note that the Z axis always lies on the joint axis, but the frame is otherwise free to "move".

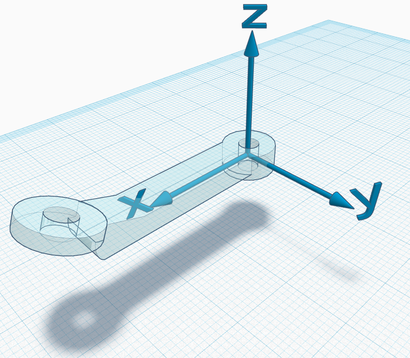
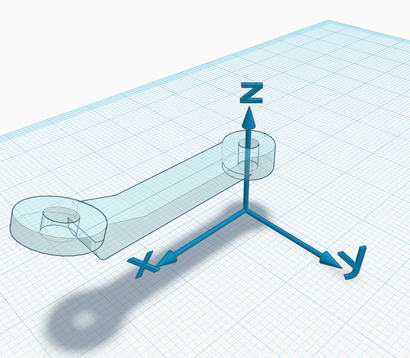
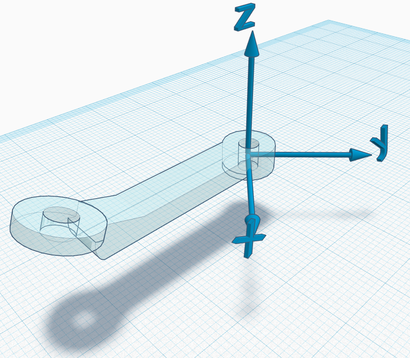
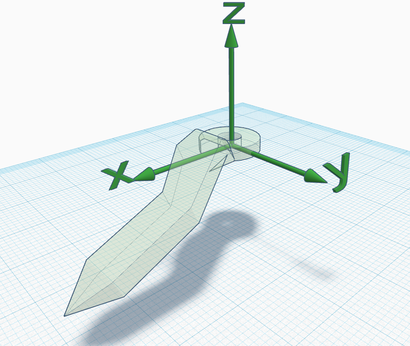
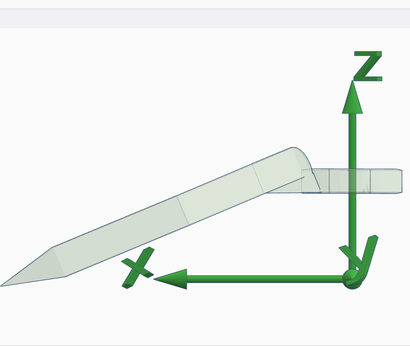
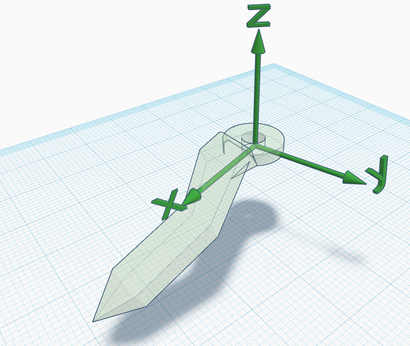
The Z axis could also be pointing in the opposite versus; the right hand rule on the Z axis determines the direction of rotation which corresponds to an increase/decrease of the joint status (choose the versus of Z to fix the preferred convention). Also, note that all combinations between the previous and these screenshots are possible, i.e., the choice of the zero configuration is independent of the choice of link frames.

4. Joint frames. At this point, the zero configuration and the link frames have been chosen. The joint frame is basically the same as the successor frame, in the zero configuration.

The two examples below illustrate the definition of a joint frame. On the left, the mechanism in the zero configuration with the link frames, and on the right the corresponding joint frame (in red) attached to its predecessor.

First example:

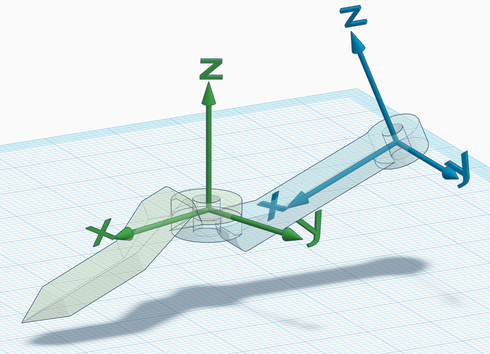
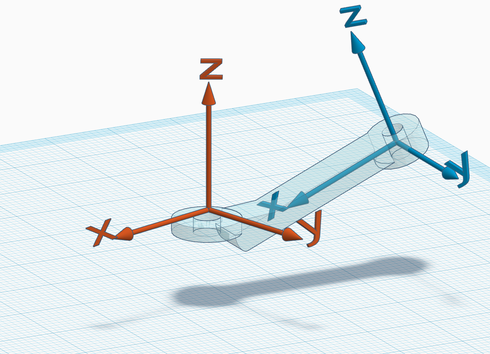
Second example:

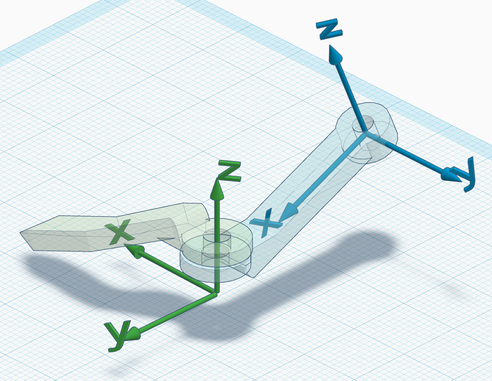
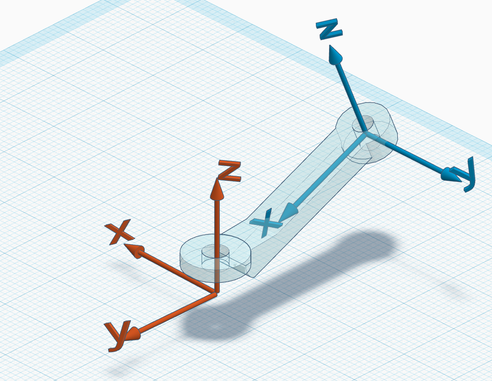
There is no need for the origin to coincide with a material point of the link, similarly as for the link frame.

5. Geometrical properties. The relative pose of the red frame with respect to the blue frame is a constant that must be included in the robot model. The previous examples would correspond to something like this:

r_joint TheJoint {
    ref_frame {
        translation = (... , 0.0, ...)  // some translation along X and Z
        rotation    = (0.0, ..., 0.0)   // rotation Y
    }
}

And in the second case:

r_joint TheJoint {
    ref_frame {
        translation = (... , 0.0, ...) // translation X and Z
        rotation    = (0.0, ..., ...)  // rotation Y and Z
    }
}

Where the dots represent a non-zero value. The complete specification of the format for the joint frame is in the next section.

Joint frame format

The ref_frame block within a joint block defines the relative pose of the joint frame with respect to the predecessor frame (which is a link frame). The pose is represented with a translation vector and with three Euler angles, representing three successive, intrinsic rotations about the X, Y and Z axis. The rotations are applied after the translation. Distances are in meters, angles in radians.

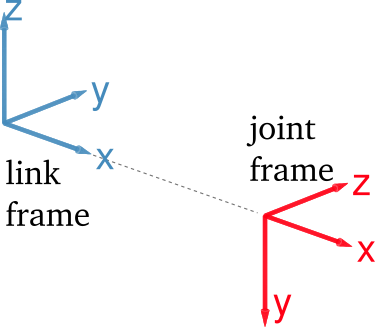
For instance, the frame of the second joint of Fancy (see above) is modeled with this text:

p_joint jB {
    ref_frame {
        translation = (1.0, 0.0, 0.0)
        rotation = (-PI/2.0, 0.0, 0.0)
    }
}

And the frames can be visualized like this:

Discussion

This is an optional section, with more information about the reference frames of the robot model.

Optional frames

More reference frames can be optionally added to any link of the model. Any frame must be defined with respect to the default frame of the link it is attached to. The format to specify the relative pose is the same as for the joint frames. The keyword for the subsection is frames. For example:

link link5 {
    // ...
    inertia_properties { /*...*/ }
    children { /* ... */ }

    frames {
        end_effector { // a custom name
            translation = ( /* ... */ )
            rotation    = ( /* ... */ )
        }
    }
}

Inertia

Any link block must specify the inertia properties of the rigid body: total mass (Kilograms), position of the center of mass (coordinates in meters), moments of inertia (Kilograms * meter squared). All the properties must be expressed in the link-frame.

link link1 {
    // ...
    inertia_properties {
        mass = 1.0
        CoM = (0.5, .0, .0)
        Ix=0.0025  Iy=0.33458  Iz=0.33458  Ixy=0.0  Ixz=0.0  Iyz=0.0
    }
    // ...
}

The example above is a model of a hollow, infinitely thin cylinder of unit length and unit mass, radius equal to 0.05. The link-frame has its origin in the center of one of the bases of the cylinder, with the x axis aligned with the height of the cylinder.

Numerical properties

RobCoGen distinguishes three classes of numerical properties/descriptors, in a robot model: variables, parameters and constants. Conceptually, the distinction is based on the average changing frequency characteristic of each class: variables change in general continuously, parameters may change, with a lower frequency, constants do not change.³

In any robot model:

• the variables are all and only the joint status variables; the variables are implicit, they do not appear in the robot model
• any numerical property of a robot model can be represented with a parameter or a constant; this is a modeling choice of the user
  • any symbolic identifier (such as mass_link1) appearing where a numerical property is expected, is considered a parameter
  • all float literals (e.g. 1.5) and expressions involving PI (e.g. PI/2.0) are considered constants

For example:

// [..]

p_joint jB {
    ref_frame {
        translation = (1.0, 0.0, 0.0)      // constant
        rotation    = (-PI/2.0, 0.0, 0.0)  // constant
    }
}
r_joint jC {
    ref_frame {
        translation = (0.0, 0.0, jC_tz)  // parameter
        rotation = (0.0, 0.0, 0.0)
    }
}

// [..]

Parametric models

If any parameter is included in a robot model, the model is said to be parametric. In this case, the model effectively represent a class of mechanisms, defined by topological equivalence.